Running While Small
Scale is everything
I keep a pet colony of the tiny ant Pheidole adrianoi on my desk. They live in a 2 mm thick layer of sand between plates of glass, and I can spy on their every move. As much as I try to seal all the possible escapes from this nest, the ants always manage a jailbreak. I now just let them wander all over my desk up to 2 meters away. Any crumb I leave on the desk is soon mobbed by foragers who cut it up and retrieve it to share with their nestmates. As I write this, a tiny worker ant is roaming an article from the New Yorker that lies on top of my computer. The ant is barely bigger than a comma.

Watching this tiny creature, I began to wonder what their world was like as they moved their tiny bodies through air. Does air have enough viscous friction to significantly resist the tiny momentum generated by their movement? If so, how does this combine with the fact that smaller animals move relatively faster, given their body size, but do so against the fluid friction of air? In the end, my inquiries revealed that the world of tiny animals is very different from ours, dominated by forces we are barely aware of, including the viscous friction of air.
I watch the ant run at a sort of “standard” speed, stopping now and then to cast about, then running again. I made a video of one running on millimeter paper so I could calculate how fast it ran by how many mm grids it crossed per second, and came up with about 30 mm per second. It wasn’t even running at top speed, but how does that compare to other things that run? Obviously, bigger animals with longer legs can run faster, so to compare them we must remove the effect of size from the calculation by expressing speed as body lengths per second. This turns the question into, “how fast can you run for your size?

Let’s start by comparing running speed. How does Pheidole adrianoi compare, for example, to my own running speed after adjusting for body size? My 2 mm long ant, ran at about 15 body lengths per second. My body length is 1.7 meters, or 1700 mm. To run at the same size-adjusted speed as the ant, I would have to run 27,000 mm per second (27 m per sec), which is almost 100 km per hour (60 mph). OK, at 82, I’m far from being a champion, but my actual, real life top speed for 100 meters is 20 seconds, which comes to only about five meters per second, or 18 km per hour (if I could run an hour, which I can’t). Despite my size (or because of it?), I am a whole lot slower than my pet ant.
Of course, the ant and I run differently, I with two legs, the ant with six. How about a fairer comparison, say with other ants, as they all run with six legs and are closer in size? Fortunately, my former student, Keith Mason measured the running speed of 15 ant species ranging from two to nine millimeters in length. His result can be seen in the graph below, to which I have added my data on Pheidole adrianoi.

Just to pick out one example, the harvester ant is four times the size of Pheidole adrianoi, so all things being equal, we might expect it to run four times as fast, but it does not. In fact, the larger the ant, the more slowly it runs, after adjusting for its size. In size-adjusted speed, the largest ants are only about one-fifth as fast as Pheidole adrianoi. For every 10-fold increase in body size, the size-adjusted running speed decreases by 86%. Of course, their actual speed is not nearly as divergent--- for example, 24 mm per second for the Florida harvester ant (Pogo bad on the graph), compared to 30 mm per second for Pheidole adrianoi.
With this information about how fast ants run, we can ask what is the importance of the resistance of air to their motion, and how does that resistance relate to their body size? Because we live in air, and air has a very low viscosity, we don’t detect much viscous resistance as we move about until we stick our head out of the window of a speeding car. This is because air is indeed a fluid, and an object moving through a fluid meets resistance (friction) to its motion. This resistance increases as fluid viscosity and/or object speed increases. Think about walking in air with its minimal viscosity and walking neck-deep in water with its much higher viscosity, and you will get the idea.
Can we measure this frictional resistance to motion? Well, with my simple equipment this would be difficult if I used ants and air. But a fluid is a fluid, and all objects moving through a fluid, be it air or water, are subject to similar forces. Thus, we can use water and steel balls to reveal these basic principles (please bear with me). Consider this set of steel balls my Found Objects. The largest weighs 100 times as much as the smallest, and because moving objects have energy in the form of momentum (inertial force), this means that at a given speed, it has 100 times as much momentum as the small one. Forces that oppose the motion, such as friction, dissipate this momentum and slow the object down. The degree of slowing is a measure of fluid friction (viscous resistance), and we can estimate it by timing the rate at which the balls fall in water while being photographed with a strobe light.

Below is the outcome in the form of a gif, using distance fallen in one second as a proxy for fluid friction. In a vacuum, all would fall at the same rate. Water slows the fall of the smallest ball much more than the largest one. The only difference among the balls is the momentum (the size and weight of the balls) and not the viscosity of the fluid. In the elapsed 0.14 seconds, the largest ball fell more than twice as far as the smallest. Friction is exerted only on the balls’ surface, and Euclid taught us that the smaller the sphere, the more surface it has per unit volume (or weight and momentum in this case). With only about 1% of the momentum, the retarding friction of water on the surface of the smallest ball is far greater in proportion to its (much smaller) momentum.
This brings me to my main point: the rate of movement of an object through a fluid depends on the ratio of the object’s momentum to the viscous resistive friction of the fluid. This ratio generally governs motion of objects in fluids.
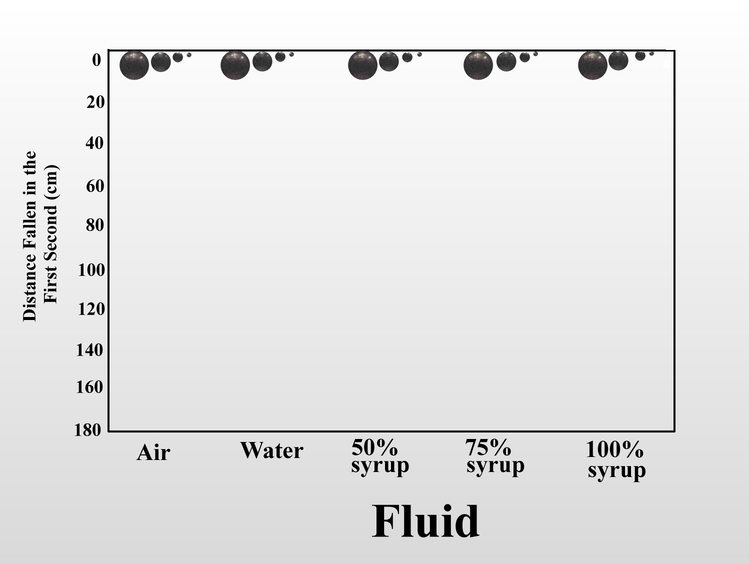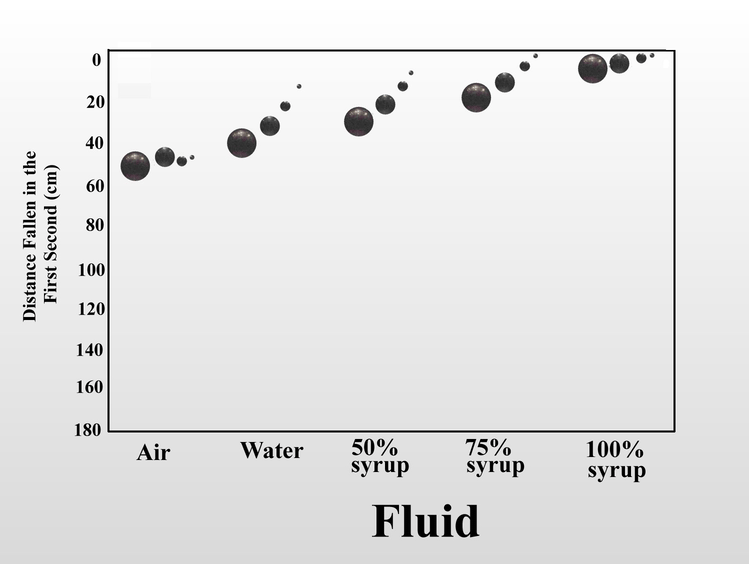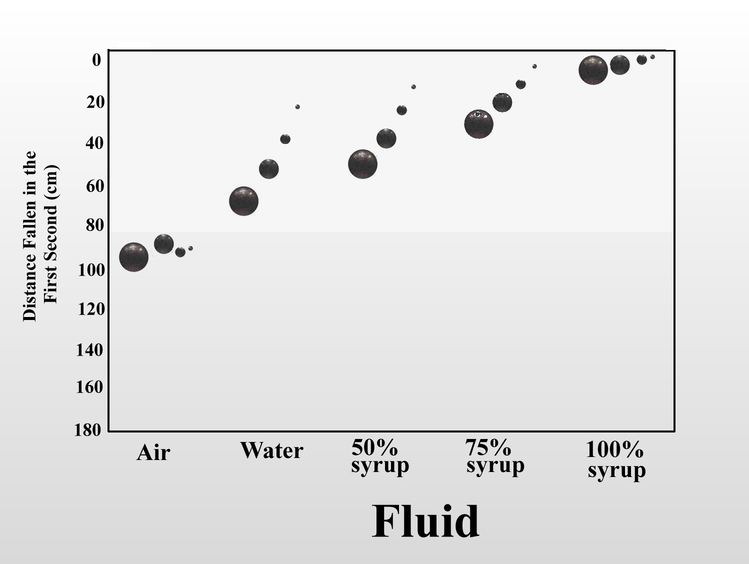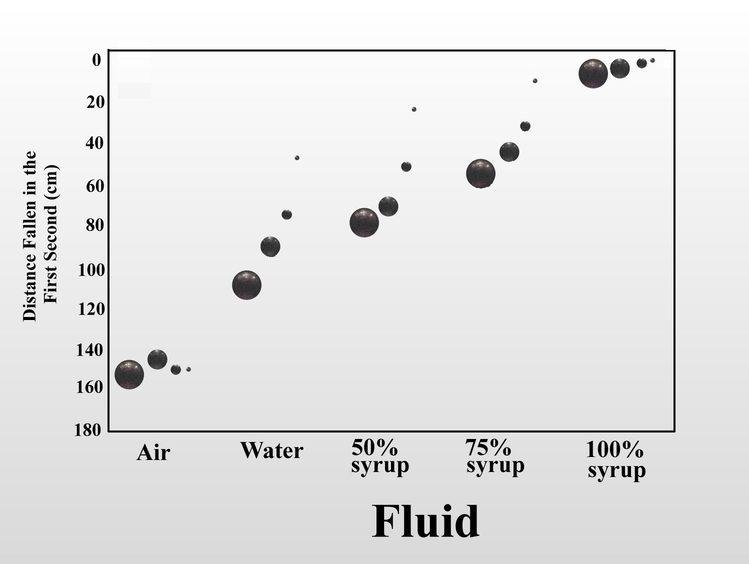
We can also increase the fluid friction on the falling object by increasing the viscosity of the fluid. When I dropped the same set of steel balls in air, water, and mixtures of Karo corn syrup in water, the distance fallen in one second serves as a proxy measure for fluid friction. In air, the four balls fall at almost the same rate, but as viscosity increased, the increased fluid friction slowed the balls in inverse relation to their size. Once again, this is because as the balls get smaller, the force of fluid friction overwhelms the decreasing momentum. In 100% syrup, the large ball falls only 6.5 cm in one second instead of 160 cm as in air, and the small ball falls less than half a centimeter. Small objects (of the same shape) are slowed more by fluid friction than large objects.
Now we can get back to ants and air--- the movement of ants through air is governed by the same forces as our falling balls, that is, momentum and fluid friction. We know the size of the ants (from 2 mm to 9 mm) and we can look up the viscosity of air, so we can calculate the ratio of momentum to fluid friction (known as Reynold’s Number) for all the ants. The result below shows that the smaller the ant, the smaller the ratio, that is, the more viscous friction predominates over momentum during the ants’ movements. For our tiny Pheidole adrianoi, this ratio is 0.21, in other words, the viscous resistance of air is five times as great as the momentum of the running ant. The ratio increases with increasing ant size, until for the largest ant, the momentum is almost five times the force of fluid friction.

For perspective, a human swimming in water at one meter per second has a Reynold’s Number of about 10,000, and in air, about one million. For a human to experience a Reynold’s Number of 0.21 as the ant does in air, the human would have to swim through honey.
This then reveals that the world experienced by this tiny ant is qualitatively different than our world. Its world is dominated by molecular forces like viscosity and cohesion, while ours is dominated by inertia, momentum and gravity. Picture it this way--- the ant is forcing its way through a rather stiff fluid, a fluid that is little disturbed by its passing, and leaves no turbulent eddies in its wake. The frictional forces of air are far greater in relation to the momentum the ant can generate with its legs. In stark contrast to our experience, air is not a “thin” fluid to our little ant. If you want a small hint of the ant’s world, try running in water, but even this does not get very close to the world of movement experienced by the ant. Whereas we occupy the same Earth, we live at such different scales that our worlds are unrecognizable to each other.
Finally, let’s extend these principles to animals that live at larger scales, say for example, the blue whale, the largest animal that ever lived. She swims through the oceans at around 10 meters per second, with a momentum/friction ratio of 10 million or so. A human swimming at about 1 meter per second experiences a ratio of 10,000. In other words, water exerts only 1/1000th (0.1%) as much retarding friction on the whale as on the human. For the whale, swimming in water must feel like moving in air does to us humans. It is hard to imagine the freedom and ease with which whales move around in their three-dimensional world.
No matter whether the size of animals is small or large, size is always accompanied by profound qualitative differences in how the world is experienced. Size matters.


All of those fascinating descriptions of the effects of scale still leave me wondering: How does Pheidole adrianoi manage to run so fast, both in terms of body lengths and actual speed? It seems like it would be the opposite...
In Rüdiger Wehner's marvelous Desert Navigator book, he describres Cataglyphus bombycina's amazing running speed- 110 body lengths per second, equivalent to a human running at 160 mph. A useful adaptation for shortening exposure time in very hot environments...