It is likely that most of us give little thought to the mechanics of drinking, although we seem to give a lot of thought to exactly what we drink. It takes me about 20 seconds to drink a glass (200 ml) of water. I just go glug glug and it flows down my esophagus, aided by gravity and my swallowing motions. If I were a quadruped, the help of gravity would be less, but the outcome would be the same.
My tiny pet ants, Pheidole adrianoi that I keep in a nest on my desk have aroused an abiding curiosity of what their experience of the world is like at their tiny scale. I wrote a piece on the realities of running when very small and figured out that when they run, air exerts significant viscous resistance to their motion. Imagine now, if even air with its very low viscosity is an impediment to the ant, then drinking liquids with their much higher viscosity must be a very different experience for them than it is for us. I set out to explore what drinking must be like when you are that small. The 19th century scientist Reynolds showed that fluid moving through a very narrow tube is greatly retarded by fluid friction with the walls of the tube, rather than sped along by the energy of motion of the fluid. His insights apply (in spades) to drinking by my tiny ants, as I will describe below.
Every sanitary engineer and plumber knows that, under constant pressure, the diameter of the pipe controls the flow rate, along with the viscosity of the fluid. The walls of the pipe exert friction on the moving liquid, slowing it near the walls to produce a streamlined flow called laminar flow. It is like cylinders sliding past one another with the slowest next to the wall and increasingly faster ones toward the center. In a large enough tube or at a high enough flow speed, the fluid toward the center becomes less streamlined until it becomes turbulent and is characterized by swirls and eddies. As the pipe diameter and flow speed decrease, the proportion of turbulent flow decreases until in very narrow pipes, it is completely laminar. In tubes as narrow as the esophagus of Pheidole adrianoi, a moving fluid would have no turbulence or eddies, no stirring or mixing (as would occur in our esophagus). The fluid moves in lockstep like a column of soldiers on a parade ground.
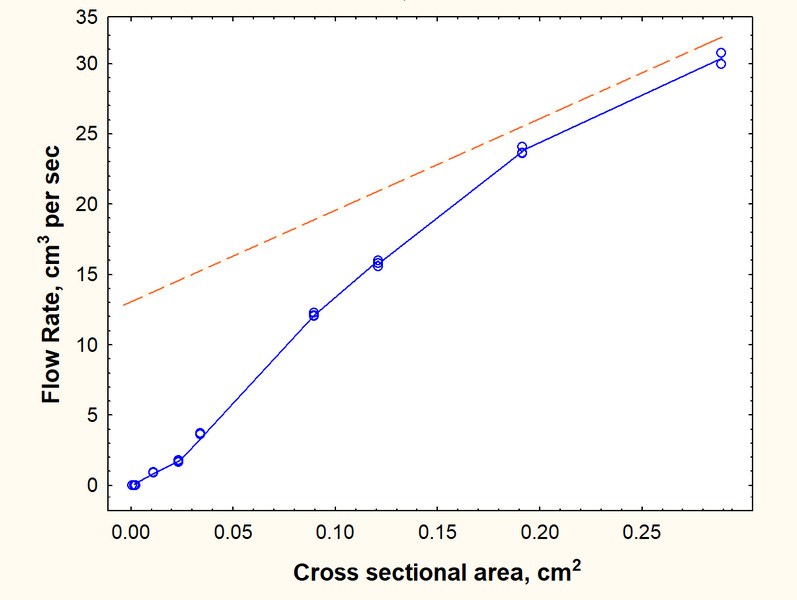
Under constant pressure, you might think that the delivery rate of fluid from the end of a pipe or tube would simply be proportional to the cross-sectional area of the tube. Half the cross-sectional area, half the flow rate, right? A testable hypothesis, right? The effect of tube diameter on flow is easy to demonstrate. I used a set of glass tubes ranging from 0.25 mm to 6 mm to drain a reservoir of water of a constant head and timed the rate at which a graduated cylinder filled up. The setup is shown below, with a single example.

Not surprisingly, the thinner the tube, the slower the flow rate (ml or cm3 per second). But the flow rate does not decrease in direct proportion to the cross-sectional area as we first expected. If the flow rates for the first two, largest tubes are representative of flow in tubes of all sizes, the red line would be a prediction of the expected flow in smaller tubes. But the actual flow rate decreases faster than the cross-sectional area. So, there must be something else going on, and that something else is the friction of the walls on the moving fluid.
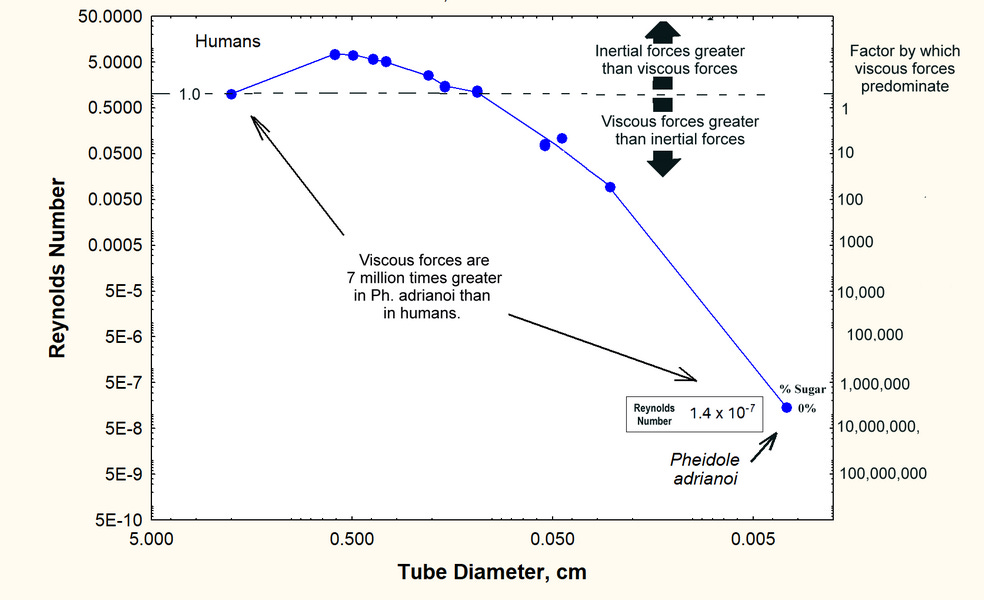
As I have written, tiny ants moving through air experience viscous friction. When they drink, it is not the ant, but the fluid that moves, with the walls of the ant’s esophagus providing viscous friction. In both running and drinking, the relevant measure is the ratio of fluid momentum to viscous friction, a ratio that is referred to as the Reynold’s Number and tells us the degree to which fluid motion is dominated by momentum or by viscous friction (below). The ratio gets very very small when the tube diameter is as small (90 micron) as it is in Pheidole adrianoi. For the sake of a comparison, when I drank that glass of water, the momentum and friction were close to the same, that is, their ratio was about 1. When Pheidole adrianoi drinks water, its very narrow esophagus means that the viscous friction on flow is about 7 million times as great as is the momentum of the moving water (ratio = 1.4 x 10-7).
Does that mean that the ants can’t drink? Obviously not, but it does mean that the experience of drinking is quite different from our own. Since my little ants regularly forage on my desk and mob every tiny crumb I leave behind, it is a simple thing to offer them a drop of sugar water. In relation to their size, it’s as if a friend asked you for a glass of water and you gave them a kiddie tub full. The ants that collect this sugar water are not really foraging for themselves, but are filling an expansible crop in their abdomen to take back to share with their nestmates by regurgitation.
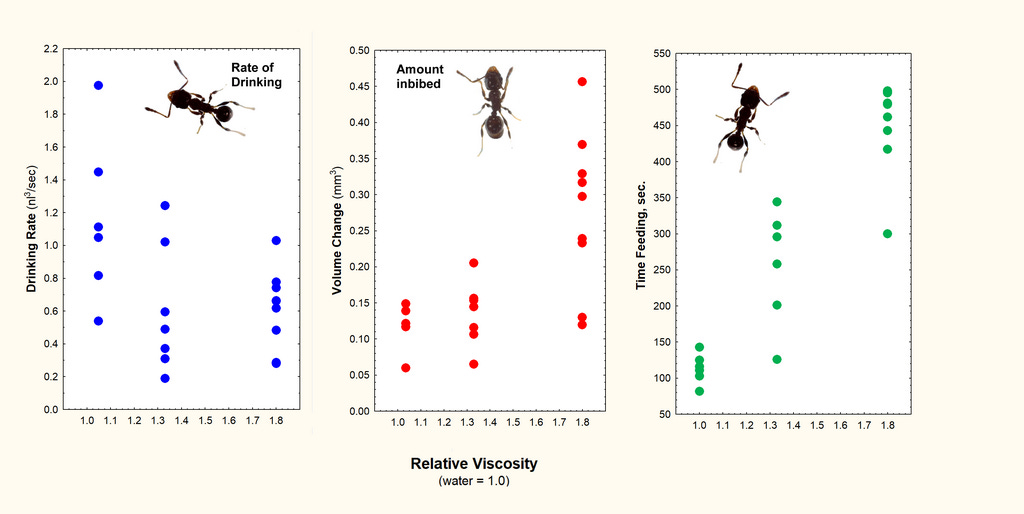
Under my digital microscope, I made videos of their feeding, allowing me to measure the increase in the volume of the abdomen as they drank, and thus to estimate both the amount they took in and the time it took. By filming them on millimeter graph paper (remember graph paper?), the videos have a scale for computing the volume of the abdomen at the beginning and end of feeding. The image below shows an example. The ants spent an average of 113 seconds imbibing the 5% sugar water, increasing their abdomen’s volume by about 130% of its initial volume. When the foragers return to their nest, they will share this volume with their nestmates.

The next question is, how do the sugar concentration and the difference in viscosity affect drinking. I offered the ants 50% and 75% Karo syrup, both obviously more viscous than water or the 5% sugar water. I used a simple (and possibly incorrect) way of judging the relative viscosity by comparing how far steel balls fall in each fluid in one second. This showed that 50% and 75%’ syrup’s viscosity was, respectively, 135% and 180% that of water. Not exactly how a fluid engineer would measure it, but sufficient for my experiments on ant drinking.
As the viscosity (and the sugar content) of the fluid increases, the ants imbibe the fluid more slowly, probably because it is more viscous, but they spend a longer time drinking and take on a larger load in their crops (below). The time spent, and the size of the final load are probably related to the higher food value of more concentrated sugar solutions. No doubt, the ants can judge the sweetness and decide how much to imbibe. They seem to be willing to trade off the extra time feeding against the higher caloric value. Of course, this is a trade-off only if their time has value, and that depends on what other opportunities they are missing or risks they are taking by feeding longer. It is my guess that over the last 140 million years, ants have become pretty good at judging such trade-offs.
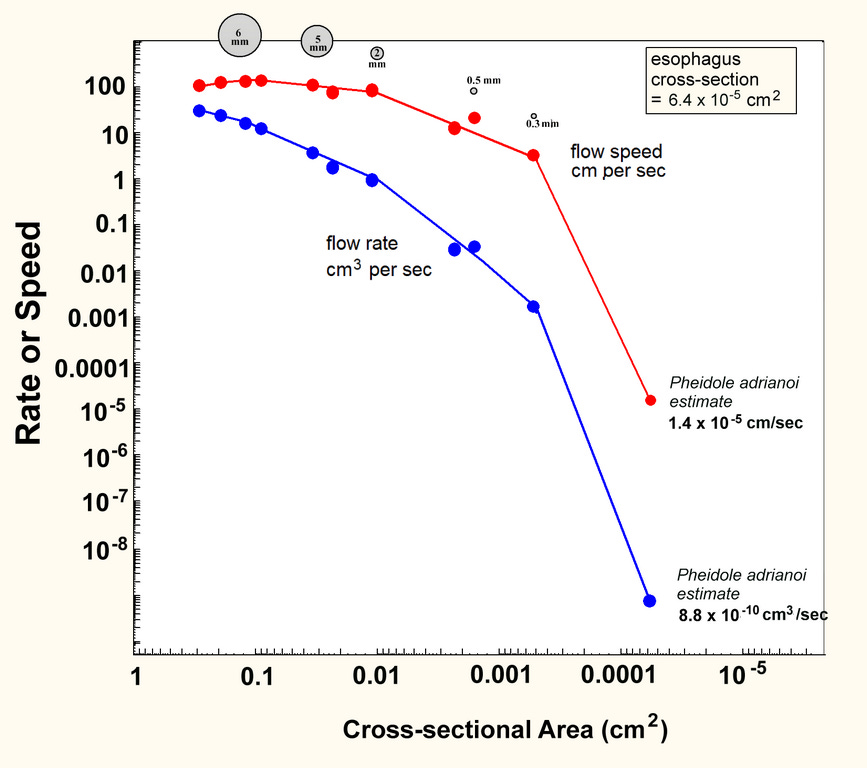
Flow rate and flow speed are not the same thing. Flow speed describes how fast an imaginary particle in the fluid (or a real one) moves down the tube (distance per second). It is calculated from the flow rate (cm3 per second) by dividing it by the cross-sectional area (cm2) to give a speed of flow (cm per second). In my measurements, when the flow rate has decreased by about one hundred-fold, the flow speed has decreased only by about 5-fold. This is necessarily so because as the tube gets thinner, fulfilling a specified volume per sec requires that the fluid move relatively faster (i.e. rate decreases faster than speed). You can see this effect in the graph below. To accommodate the large range of values, I have plotted the logs of both. The flow rate and the flow speed expected for Pheidole adrianoi from its esophagus cross-sectional area (9.1 x 10-6 cm2) are shown.
We can get more insight into what the ant is up against when it drinks. When the fluid is water, the viscous resistance to flow is over 7 million times as great as the fluid momentum. To have a similar experience, we humans would have to imbibe a fluid 7 million times as viscous as water. What might such a fluid be? An internet search revealed that toothpaste is about 100,000 times as viscous as water. To picture what the ant is doing, imagine sucking up toothpaste with a straw, and then picture that the ant is actually sucking up a fluid whose resistance to flow is 100 times as great.
But I wasn’t offering the ants water, I was offering them sugar solutions some of whose viscosity was far greater than water’s, which means that the ratio of fluid momentum to viscous friction was much smaller still. How does the ant accomplish this feat? How does it apply the necessary force to move the liquid through its pharynx and into its esophagus and crop? As in most insects, the ants have two pumping structures associated with the pharynx in their heads, the first is just downstream from the mouth (the cibarial pump) and the next is right behind it (the pharyngeal pump). Both move liquid by repeated muscular contractions that lift the top of the pharynx tube like bellows to create a vacuum that sucks in the liquid and pushes it along as the muscles relax. The pharyngeal pump fires just after the cibarial one to create a one-way pumping system that moves the fluid back toward the crop and prevents it from flowing back out the mouth. When we swallow, the peristaltic movements have much the same effect, but a crucial difference is that the moving column of fluid is turbulent in our case, but laminar in the ant’s case, more like pushing a stiff fluid down a tube, and probably a lot more work.
Scale is a crucial feature of the experienced worlds of all creatures, from microscopic to colossal. These worlds are so different that we hardly recognize them, and must resort to thought experiments like this one to try to imagine these other worlds. We can’t be blamed for being scale-chauvinists, but imagining the worlds of other creatures makes us aware of the worlds within worlds that make up life on earth.



This essay is a deep dive into a tiny world. So much to think about. Thanks!
Walter,
As usual your essay was interesting, albeit the math was multistories above my head. Regrettably, I lack either of the pumps needed to push the math into my brain. You would not need graph paper to check for expansion: There ain't any.
On a serious note, the last paragraphs on the pump mechanisms, without the daunting math, were the most interesting and graspable to me. Steve